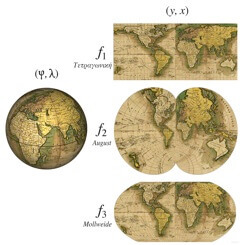
«Η επίπεδη εικόνα της γήινης σφαίρας σε σμίκρυνση» είναι η απλούστερη απάντηση στο απλό ερώτημα «τί είναι χάρτης;». Η απλούστερη, αλλά ίσως πιο συγκεκριμένη και πεζή από τους πολλών βαθμών ελευθερίας λογοτεχνικούς και φιλοσοφικούς ορισμούς ή τους λιγότερων βαθμών ελευθερίας αλλά πολύπλοκους ακριβέστερους επιστημονικούς. Συνήθως την απλούστερη απάντηση στο απλό ερώτημα ακολουθεί το εξίσου απλό ερώτημα «κι αυτό πώς γίνεται;». Και η απλούστερη απάντηση γίνεται όλο και πιο σύνθετη από την προηγούμενη. Και αν ο περίεργος συνεχίσει την ακολουθία των απλών ερωτημάτων τότε θα δέχεται πολυπλοκότερες απαντήσεις που ή θα τον απομακρύνουν τελικά από τις απορίες του επειδή θα βαρεθεί ή θα μπερδευτεί ή θα κεντρίσουν την περιέργειά του, που μακραίνει την ακολουθία των ερωτήσεων. Γιατί ως γνωστόν η περίεργη, ο περίεργος ή η περιέργεια δεν είναι μόνο κίτρινη ή μπλε, δεν σκοτώνει μόνο γάτες ή εμπλουτίζει το κουτσομπολιό στη γειτονιά, αλλά και προάγει την αυτοβελτίωση, τη γνώση και γιατί όχι, την αγάπη των χαρτών!
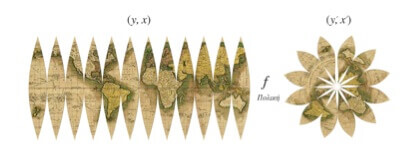
Στο θέμα μας όλα ξεκινάνε από ένα παράδοξο (κάτι που συμβαίνει αλλά ακούγεται απίστευτο) ή παράξενο (κάτι που δεν μας είναι γνωστό και οικείο), το οποίο όμως προσθέτει πολλά στη «μαγεία των χαρτών» που μας αρέσει να πιστεύουμε ότι υπάρχει: η φυσική επιφάνεια μιας σφαίρας δεν μπορεί ποτέ να γίνει επίπεδη, χωρίς να «καταστραφεί», χωρίς να κοπεί, χωρίς να αλλοιωθεί. Αν το κόψιμο γίνει σωστά, οργανωμένα και με τάξη, δηλαδή «καθώς πρέπει», τότε το κομμένο επίπεδο μπορεί να ξαναγίνει σφαίρα! Επομένως το «καθώς πρέπει» είναι ένα σωστό κόψιμο της επιφάνειας της σφαίρας. Η ανθρώπινη διάνοια επινόησε, ως «καθώς πρέπει», το κόψιμο σε δώδεκα σφαιρικές ατράκτους εύρους 30 μοιρών, όπως φαίνεται στο Σχ. 1.